CUDAによるジュリア集合の描画

　定期試験も来週に迫っているわけであるが、凝りもせず、こんな駄文をインターネットに垂れ流している。というのも、今週にもあった定期試験を対した努力もせず、パス出来たからである。人間というのは、楽な課題だけ選んで挑戦していれば、努力せずともそこそこの成果を得られてしまう、それだけならいいのであるが、結果を得ることで自分が優秀な人間であると勘違いしてしまうことがある、これは恐ろしいことである。知らず、知らずのうちに能力がどんどん下がっていってしまうからである。

　僕は以前も書いたように豊橋技科大のコンピュータクラブに所属しプログラムを書いているわけであるが、ゲームのような一般人から見てもわかりやすいものを作っているわけでも無く、文化祭の際にこれといって展示できるようなものが無かったた。以前からCUDAとOpenCVによる画像処理を行っていたため、CUDAのカーネルを記述することが出来た。そこでCUDAを用いてマンデルブロ集合やジュリア集合と言ったフラクタルを描画するプログラムを作成した。

１．フラクタル

　こんなブログを訪ねてくる人であれば大抵フラクタルについて理解はしているであろうが、一応簡単に説明しておく、僕はその分野の数学を専攻した事が無いので詳しい概念を理解しては居ないのだが、簡単に言うと無限の階層を持つ自己相似形の集まりである。

　分からない人は、そんなことを言っても分かりづらいと思うので、身近な例を挙げるとブロッコリーやカリフラワーの構造であろう。サラダに入っている小さく切られ、茹でられたブロッコリーと、スーパーで売られているブロッコリーは相似形である。更に、サラダに入っている茹でられたブロッコリーの一部を手でちぎると、そのかけらはサラダに入っているブロッコリーの切れ端とも、スーパーで売られているブロッコリーとも相似形である。簡単にいうと一部と全体の形が同じなのである。

　ブロッコリーはちぎっていくとつぼみ一つ一つになってしまうため、階層は有限であるが、数式で記述されるフラクタル図形は計算時間とアウトプットの解像度が許す限り無限の階層を持つことができる。

２．ジュリア集合とマンデルブロ集合

　僕は実際この集合の数学的な意味に関しては理解出来ていない、ただ映しだされる模様が美しいので好きなのである。次の画像がジュリア集合を描画した一例である。これは僕が作成したプログラムで描画したものである。

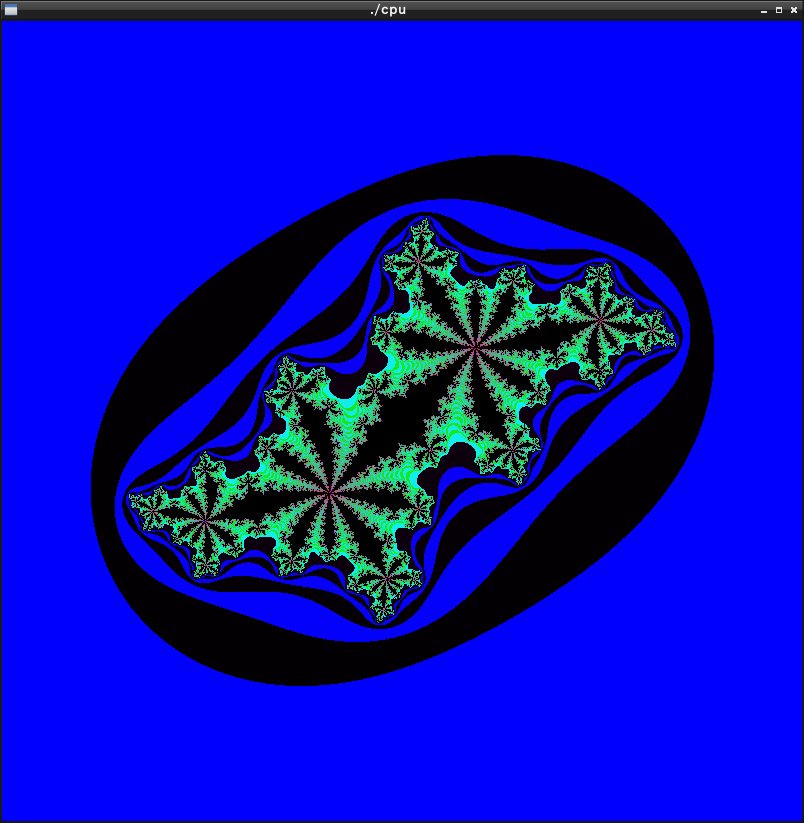
ジュリア集合は次の式で表される。

　この計算を繰り返していくと、Zの値が変化し、発散する場所が出てくる。それに必要な計算回数をプロットしていくと以上の様な幾何学模様が現れるのである。というのは複素数のでありという定義からX座標Y座標さえあれば計算することができる。

　このへんは数式で考えると頭が痛くなってくるので後々プログラムで説明するが、この計算の初期パラメータを変化させることで、ジュリア集合は様々な形に変形し、美しい幾何学模様を描くのである。

3.実装

　今回作成したプログラムは前節せ説明したパラメータを変化させジュリア集合の形が変化していくのを描画するだけのものである。様々に変化するジュリア集合の美しい模様を観察することができる。

　CUDAのカーネルは通常のC++と別に.cuファイルを作る必要があるため実装は2つのファイルに分けて行った。一つ目がOpenGLで描画を行うC++ファイル、2つ目がGPGPU計算を行うCUファイルである。

man.cu

#include "man.cuh"
#include "config.h"
#include <cuda_runtime.h>
#include <stdlib.h>
#include <stdio.h>
#include <malloc.h>
#include <device_launch_parameters.h>
#define BLOCK 32

__global__ void cal_pix(float* inMatA,float ci);

void draw_gpu( float *ptr_h){
	int matrixSize = sizeof( float) * V_MAX * (H_MAX*3) ;
	float* hMatA;
	hMatA = (float*)malloc(matrixSize);
	int col, row;
       //初期化
	for(col = 0; col < V_MAX; col++){
		for(row = 0; row < H_MAX; row++){
			hMatA[(col * H_MAX + row)*3 + 0] = 0;
			hMatA[(col * H_MAX + row)*3 + 1] = 0;
			hMatA[(col * H_MAX + row)*3 + 2] = 0;
		}
	}
	float* dMatA;
	cudaMalloc((void**)&dMatA,matrixSize);
	cudaMemcpy(dMatA,hMatA,matrixSize,cudaMemcpyHostToDevice);
	dim3 block(BLOCK, BLOCK);
	dim3 grid(V_MAX / BLOCK,H_MAX / BLOCK);

	static double cnt = 0.0;
 	cnt = cnt +0.01;
	double cir = sin(cnt) * 0.5;
        //カーネルの呼び出し
        cal_pix<<< grid, block >>>(dMatA,cir);
	cudaThreadSynchronize();
	cudaMemcpy(ptr_h,dMatA,matrixSize,cudaMemcpyDeviceToHost);
	free(hMatA);
	cudaFree(hMatA);
	cudaThreadExit();
}

__global__ void cal_pix(float* inMatA,float ci){
	int col = blockIdx.x * blockDim.x + threadIdx.x;
	int row = blockIdx.y * blockDim.y + threadIdx.y;
	float x,y,xx,yy,zr,zi;
	double l;
	x = (3.0)*((float)col/V_MAX) - 1.5;
	y = (3.0)*((float)row/H_MAX) - 1.5;
	xx = x;
	yy = y;
	for(l = 0; l < 16; l+=0.05){
		zr = xx*xx - yy*yy +ci;
		zi = 2*xx*yy+0.64;
		xx = zr;
		yy = zi;
		if((zr*zr + zi*zi) > 4) break;
	}	
	inMatA[(col * H_MAX + row)*3 + 0] = (l > 15.5)? 0: l/16;
	inMatA[(col * H_MAX + row)*3 + 1] = (l > 15.5 || l < 1.0)? 0: (16 - l )/16;
	inMatA[(col * H_MAX + row)*3 + 2] = ( (int)(l*20) & 1)?  l/16: (16 - l )/16 ;
}

　CUDAカーネルはｃ＋＋ファイルから呼び出す事が出来ないので間にdraw_gpu関数を挟む、この関数はGPU上に渡す画像の配列データとの初期化を行い、cal_pix関数へ渡す。この関数は渡された情報を基に自分の担当するピクセルがどのような条件で発散するかを調べ配列データに格納する。

gpu.cpp

#include <GL/glut.h>
#include "config.h"
#include "man.cuh"
#include <math.h>
#include <stdio.h>
float vram[(V_MAX * H_MAX)*3];

void idle(void)
{
  glutPostRedisplay();
}
void display(void)
{
  static float cnt = 0;
  cnt = cnt + 0.01;
  int i=0,j=0;
  glClear(GL_COLOR_BUFFER_BIT);
  glBegin(GL_POINTS);
  int pos;
  draw_gpu(vram); 
  for(i = 0; i < V_MAX ; i++){
	for(j = 0;j < H_MAX; j++){
	  pos = ((V_MAX * i) + j) * 3;
	  glColor3d(vram[pos+0] , vram[pos+1], vram[pos+2]); /* 赤 */
          glVertex2d(4.0*((float)i/V_MAX) - 2.0 ,4.0*((float)j/H_MAX) - 2.0);
	}
  }
	  
  glEnd();
  glutSwapBuffers();
}

void resize(int w, int h)
{
  glViewport(0, 0, w, h);
  glLoadIdentity();

  glOrtho(-w / (V_MAX/2), w / (V_MAX/2), -h / (H_MAX/2), h / (H_MAX/2), -1.0, 1.0);
}

void init(void)
{
  
}

int main(int argc, char *argv[])
{
  glutInitWindowSize(V_MAX, H_MAX);
  glutInit(&argc, argv);
  glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);
  glutCreateWindow(argv[0]);
  glutDisplayFunc(display);
  glutReshapeFunc(resize);
  init();
  glutIdleFunc(idle);
  glutMainLoop();
  return 0;
}

 main.cppファイルはcudaを呼び出し描画するだけの簡単な処理を行う関数である。描画はOpenGLによって行っており、表示にはGULTを使用している。

　コンパイルは次のMakefileで行った

gpud: man.o gpu.o
	nvcc  -O2 -o gpu gpu.o man.o -lglut -lGLU -lGL -lm
gpu.o: gpu.cpp man.cuh config.h
	nvcc -arch=sm_20 -c  gpu.cpp -lglut -lGLU -lGL -lm
man.o: man.cu man.cuh config.h
	nvcc -arch=sm_20 -c man.cu
clean:
	rm man.o gpu.o

　CUDAを使って計算してみて驚いたことは、CUDAで計算してCPUに書き戻すまでのオーバーヘッドが思ったよりも大きかったことである。結果として発散までの計算回数が少ない場所ではCPUでジュリア集合の計算を行った場合に比べ、CPUで計算したほうが高速な部分が見受けられた。これには少し落胆してしまった。（とは言っても僕が使用しているGPUがGTX720というintelHDに毛が生えたレベルなのが原因かもしれないが）